Логистика — одна из самых затратных статей бюджета компании. Она оказывает существенное влияние на себестоимость производимых и поставляемых товаров, объем и рентабельность бизнеса, оборачиваемость товарных запасов, качество обслуживания клиентов и их лояльность. Правильно выстроенное управление логистикой позволяет увеличить годовую прибыль компании и экономить до 30% от всех затрат на процесс. Попробуем рассмотреть реальные задачи из области стратегического планирования логистики, а также принцип работы решающего их мат.аппарата.
Нередко логистику рассматривают с позиции управления транспортными перевозками товара или сырья из пункта А в пункт Б. Тем не менее это намного более комплексный процесс, включающий в себя прогнозирование объемов продаж, управление распределением и пополнением товаров и сырья, складскими запасами, производством, планирование логистических маршрутов и пр. Столь комплексная задача не может быть тривиальной, в ходе ее решения нередко возникают вопросы – «А что, если..?». Например, а что если нам построить новый склад? Перейти на другую схему логистики? А что будет, если увеличатся импортные пошлины? Поставщики поднимут ставки? Повысится курс доллара? Подобные вопросы лежат в области стратегического планирования и моделирования. Цели могут быть разные – от оптимизации или ускорения процессов до получения максимальной прибыли.
Если задача разовая, характеризуется ограниченным набором вводных, и встает перед небольшой гибкой компанией, то ее можно решить в Excel. Для крупных территориально распределенных компаний, где логистика – один из ключевых бизнес-процессов, от которого зависит рентабельность всего бизнеса, даже одноразовые задачи могут содержать до нескольких миллионов начальных данных. Решать их в Excel уже проблематично. Для решения задач оптимизации существуют специализированные виды софта. Они есть как у ведущих производителей ПО, таких как Oracle, JDA, IBM, SAP, так и у ряда специализированных компаний – например, Riverlogic и QlickView. Альтернативный вариант – кастомизированные решения российских компаний (в том числе и КРОК), построенные на базе open source продуктов. Кстати говоря, использовать некоторые из решений можно и в качестве облачного сервиса с оплатой только за фактическое использование и начальную настройку модели. В частности, похожее SaaS-решение потребляет из нашего облака одна производственная компания с целью планирования производства и распределения сырья по производственным площадкам.
Примеры задач
Например, для одного крупного дистрибьютера мы разработали модель цепочки поставок, включающую всех поставщиков и склады в филиалах компании. Теперь заказчик может моделировать материальные потоки и различные виды затрат, возникающие при движении товаров, а также накладывать ограничения на логистические мощности.
Так, в числе задач - поиск оптимальных размеров заказов и типов упаковки для межскладских перемещений и закупок у поставщиков, а также анализ целесообразности коммерческих завозов с учетом различных бонусных условий, предоставляемых поставщиками за закупленные объемы или под будущее повышение цен.
Рассмотрим простой пример -поставщик объявил о повышении цен на всю продукцию на 10%, начиная с 2015 года:
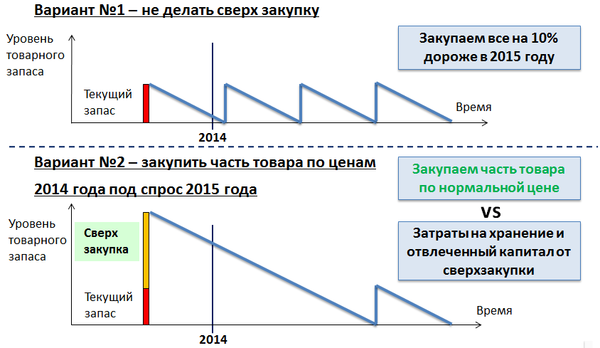
В качестве результата моделирования был получен оптимальный план закупок до конца 2014 года по каждой товарной позиции, обеспечивающий максимальную экономию с учетом будущего повышения цен и минимальные затраты на хранение и иммобилизацию активов в запасах.
Из других задач можно привести пример, интересный производственным компаниям с целью получения максимальной прибыли. Так, компаниям-производителям алкогольной продукции важно понимать – сколько, на каком заводе и какой сорт продукции производить. Почему это важно? Например, потому что у одного завода может быть очень низкая себестоимость производства, но при этом он далеко расположен. Системы автоматизации позволяют решить и такие задачи.
В связи с экономической обстановкой участились и разовые запросы на моделирование той или иной ситуации, которые мы решаем в рамках экспресс-услуг. Например, оптимизация логистических маршрутов, которые должны прокладываться с учетом расстояния между складами, скорости движения, времени отдыха водителей, оптимальными стоимостью погрузки/разгрузки машины и временем этих операций для каждого склада. Или другая разовая задача – оптимизация затрат на строительство склада. Вопрос - где его лучше строить - в регионе с дешевой землей, но с дополнительными затратами на доставку, или в Подмосковье, где земля дорогая, но доставка до основных потребителей окажется дешевле и быстрее. Правильно подобранный математический аппарат помогает взвесить все за и против.
Вообще говоря, на похожем математическом движке могут решаться и нелогистические оптимизационные задачи, такие как оптимизация работы задвижек на тепловой станции, расстановка посадочных мест в самолете, расчет оптимальной огранки алмазов и пр.
Как это работает?
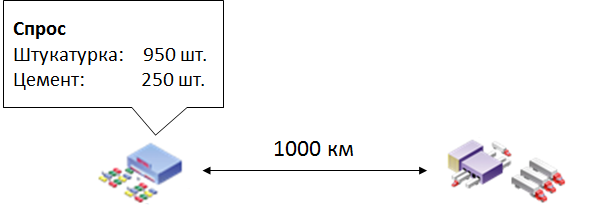
О том, как работают системы оптимизации, не знают даже многие эксперты в области логистики. Поэтому небольшой ликбез может быть многим полезен или как минимум интересен. Представим самую простую ситуацию. У компании есть распределительный центр (РЦ) и склад магазина, куда из РЦ нужно доставить товары. Товаров для простоты всего два – цемент и штукатурка. Известен недельный спрос магазина, и объем мощностей, которые имеются в нашем распоряжении – это фуры грузоподъемностью в 20 тонн. Все остальные справочные данные приведены на схеме ниже.
Параметр
Значение
Обозначение
Продажа 1 шт. Штукатурки, чистая выручка
80 руб
СшПродажа 1 шт. Цемента, чистая выручка
50 руб
СцВес Штукатурки 1шт
30 кг
wшВес Цемента 1шт
40 кг
wцШтукатурка, штук в упаковке
20 шт
uшЦемент, штук в упаковке
12 шт
uцГрузоподъемность транспорта
20 000 кг
WПогрузо-разгрузочные работы на фуру
3 000 руб
R0Стоимость доставки за 1 км
20 руб
R1
Перед нами стоит задача определения количества транспортных средств и их загрузки с целью максимизации прибыли (на самом деле критериев для оптимизации может быть множество – это и сокращение затрат, и минимизация времени доставки и другие).
Выбранный нами критерий оптимизации формализуется в виде целевой функции:
Aшсшиш + Ацсциц - RТ → max
Другими словами, мы хотим подобрать такие объемы поставки Аш и Ац (количество упаковок каждого товара), чтобы получить максимальную прибыль от реализации товара.
Здесь RТ – суммарная стоимость перевозки груза, в нашем примере фиксированная, но, вообще говоря, это необязательно:
RТ = R0 + 1000 * R1 = 23 000 руб
При этом нам необходимо соблюсти ряд ограничений. Например, суммарный вес перевозимого фурой товара не должен превышать ее грузоподъемности:
Ашwшиш + Ацwциц ≤ W
Суммарный объем поставки по каждому товару не должен превышать его спроса на этот товар B (по условиям нашей задачи, в жизни это не всегда так):
Ашиш ≤ Вш, Ашиш ≤ Вц
Есть и несколько моментов, понятных любому специалисту, но абсолютно безразличных компьютеру. Например, важно задать, чтобы объемы поставок каждого товара были неотрицательными:
Аш ≥ 0, Ац ≥ 0
И, разумеется, количество упаковок товара должны быть целым числом (компьютеру это также необходимо задать). Дальше составляется и решается финальная система из 4 выделенных уравнений. Вопросы решения таких задач (они называются экстремальными) изучает специальный раздел математики – математическое программирование. Наш подкласс задачи один из самых простых и называется целочисленным линейным программированием.
Так вот, решая эту задачу с помощью какого-то из математических пакетов (например, IBM CPLEX, Gurobi, Matlab и др.) мы получаем такое решение:
А1ш = 33, А1ц = 0
В бизнес-плоскости мы получаем оптимальную загрузку первой фуры, перевозящей 19 800 кг товара. Соответственно, доставка приносит 29 800 рублей чистой прибыли.
Остаток спроса составляет:
В1ш = Вш - А1шиш = 290 шт, В1ц = Вц - А1циц = 250 шт
Эти данные используются для расчета второй, абсолютно аналогичной системы уравнений. Оптимальное решение имеет следующий вид:
А2ш = 14, А2ц = 20
Таким образом, мы выяснили, что вторая фура перевозит 18 000 кг товара, и доставка принесет 11 400 рублей чистой прибыли. Остаток спроса:
В2ш = В1ш - А2шиш = 10 шт, В2ц = В1ц - А2циц = 10 шт
Достаточно легко убедиться, что удовлетворение остаточного спроса магазина приводит к убыткам, а значит, при данных ограничениях мы не удовлетворяем полный спрос магазина (формируем дефицит товара), но при этом сохраняем максимальную прибыльность.
Здесь крайне важно вспомнить об ограничениях. А что если мы снимем ограничение Аiиi ≤ Вi, т.е. позволим формироваться профициту товара? Разумеется, при этом разумно учесть уменьшение прибыли с товара за счет стоимости его хранения. В нашем примере мы учтем этот факт в виде 50% дисконта на профицитный товар. Это приводит к тому, что стоимость товара перестает быть в наших уравнениях постоянной величиной и становится функцией, к тому же еще связанной с количеством упаковок товара:
![]()
При введении нового ограничения (кстати говоря, нелинейного, что усложняет решение задачи), изменяется оптимальное количество упаковок для второй фуры и составляет уже:
А2ш = 16, А2ц = 21
При этом вторая фура перевозит 19 680 кг, ожидаемая прибыль составляет 13 300 рублей (на 1 900 рублей больше с учетом дисконта на профицитный товар). Есть над чем подумать логисту…
Подводим итоги
Естественно, то, что мы проделали выше, является достаточно упрощенным примером того, что происходит в реальных системах, но надеемся, поможет приоткрыть завесу тайны над «внутренностями» систем оптимизации и начать доверять им больше. Соответствующие ИТ-решения позволяют не просто оптимально спланировать процессы, но и сделать так, чтобы затраты на логистику оказались минимально возможными - сократить их целые десятки процентов.

Анастасия Гончарова, руководитель направления систем управления цепочками поставок компании КРОК

Роман Чеботарев, ведущий консультант по внедрению бизнес-приложений компании КРОК





